Next: The ``Mountain'' function
Up: Method
Previous: Regularization: Moving Least Squares
The fiber tract trajectory
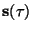 can be computed as a
parametric 3D curve through linear integration of the filtered principal eigenvector:
can be computed as a
parametric 3D curve through linear integration of the filtered principal eigenvector:
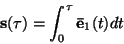 |
(26) |
where 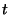 is a parameter of the curve and has corresponding
is a parameter of the curve and has corresponding
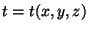 values and
values and
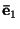 is the MLS filtered principal
direction (unit) eigenvector as a function of position.
is the MLS filtered principal
direction (unit) eigenvector as a function of position.
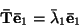 |
(27) |
The discrete integration can be done numerically using explicit or implicit
methods depending on the converging/diverging nature of the tensor field. The simplest approaches are a forward (for diverging fiber fields)
![\begin{displaymath}
\mathbf{r}_{new} = \mathbf{r}_{old} + \mathbf{ \bar e}_1[\mathbf{\bar T}(\mathbf{ r}_{old})]
\Delta t
\end{displaymath}](img115.gif) |
(28) |
or inverse Euler schemes (for converging fiber fields):
![\begin{displaymath}
\mathbf{ r}_{new} = \mathbf{r}_{old} + \mathbf{\bar e}_1[\mathbf{\bar T}(\mathbf{ r}_{new})] \Delta t
\end{displaymath}](img116.gif) |
(29) |
One can easily employ higher order integration schemes, but they
still should be chosen according to the local properties of the tensor field
(converging or diverging) that are associated with the ``stiffness'' of
the differential equation, bifurcations and the desired geometry.
Next: The ``Mountain'' function
Up: Method
Previous: Regularization: Moving Least Squares
Leonid Zhukov
2003-01-05