Next: Streamline Integration
Up: Method
Previous: Data Interpolation
To perform a stable fiber tracing on experimental data, the data needs
to be filtered. A simple global box or Gaussian filter will not work
well, since it will blur (destroy) most of the directional information
in the data. We also want the filter to be adjustable to the data and
be able to put more weight on the data in the direction of the traced
fiber, rather than between fibers. We also want the filter to have an
adjustable local support, which can be modified according to the
measure of the confidence level in the data. Finally, we want the
filter to preserve sharp features where they exist (ridges), but
eliminate irrelevant noise if it can. Thus, to do this, the behavior
of the filter at some voxel in space will depend on the ``history of
the tracing'', (where it came from), so the filtering needs to be
tightly coupled with the fiber tracing process.
Due to the above reasons, we chose to use a moving least squares (MLS)
approach. The idea behind this local regularization method is to find
a low degree polynomial which best fits the data, in the least squares
sense, in the small region around the point of interest. Then we
replace the data value at that point by the value of the polynomial at
that point
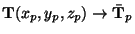 . Thus, this is a data approximation rather than an
interpolation method. The measure of ``fitness'' will depend on the
filter location, orientation and the history of motion. The one
dimensional MLS method was first introduced in signal processing
literature [9,17].
We start the derivation by writing a functional
. Thus, this is a data approximation rather than an
interpolation method. The measure of ``fitness'' will depend on the
filter location, orientation and the history of motion. The one
dimensional MLS method was first introduced in signal processing
literature [9,17].
We start the derivation by writing a functional
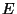 that measures the
quality of the polynomial fit to the data in the world coordinate
system. To produce E, we integrate the squared difference between
that measures the
quality of the polynomial fit to the data in the world coordinate
system. To produce E, we integrate the squared difference between
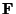 , which is an unknown linear combination of tensor basis
functions, and
, which is an unknown linear combination of tensor basis
functions, and
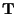 , the known continuous trilinear
interpolated version of given tensor data. We integrate over all of 3D
space and use weighting function
, the known continuous trilinear
interpolated version of given tensor data. We integrate over all of 3D
space and use weighting function
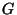 to create a region of interest
centered at chosen 3-D point
to create a region of interest
centered at chosen 3-D point
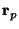 with coordinates
with coordinates
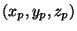 :
:
|
![$\displaystyle E({\mathbf r}_p) =
\int_{-\infty}^{\infty} G({\mathbf r}-{\mathbf...
...hbf F}({\mathbf r}-{\mathbf r_p}) - {\mathbf T}({\mathbf r})]^2
~d{\mathbf r}^3$](img53.gif) |
|
|
(8) |
The second argument
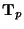 (value of the tensor at the
center point) of the weighting function
(value of the tensor at the
center point) of the weighting function
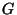 determines the weighting
function's size and orientation.
The square of the tensor difference in (8) is a scalar,
defined through the double-dot (component wise) product
[4,3]:
determines the weighting
function's size and orientation.
The square of the tensor difference in (8) is a scalar,
defined through the double-dot (component wise) product
[4,3]:
|
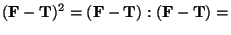 |
|
|
(9) |
|
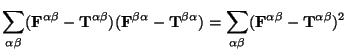 |
|
|
|
Figure 4:
Coordinate systems used by linear transformation Eq.
 to change from
to change from
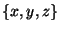 coordinates in Eq.
coordinates in Eq.
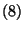 into
into
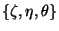 coordinates in Eq.
coordinates in Eq.
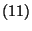 .
.
Within the functional
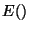 , the tensor function
, the tensor function
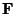 is a
linear combination of tensor basis functions we will use to fit the data. The
function
is a
linear combination of tensor basis functions we will use to fit the data. The
function 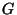 is the moving and rotating anisotropic filtering window,
centered at the point
is the moving and rotating anisotropic filtering window,
centered at the point
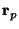 (See Figure 4.)
We felt it was more convenient to perform the computations in the
local frame of reference connected to a particular filtering window,
rather than in world coordinates. It is straightforward to transform
equation (8) to a local frame of reference using a
change of variables involving the following translation and rotation
transformation:
(See Figure 4.)
We felt it was more convenient to perform the computations in the
local frame of reference connected to a particular filtering window,
rather than in world coordinates. It is straightforward to transform
equation (8) to a local frame of reference using a
change of variables involving the following translation and rotation
transformation:
|
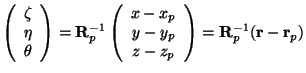 |
|
|
(10) |
where
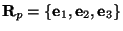 is a rotation matrix formed by the eigenvectors of the tensor
is a rotation matrix formed by the eigenvectors of the tensor
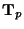 at the point
at the point
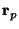 . Then, in the local
frame of reference,
. Then, in the local
frame of reference,
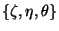 , the equation
(8) becomes
, the equation
(8) becomes
|
![$\displaystyle E = \int_V {[ {\mathbf F}({\mathbf R}_p \{\zeta,\eta,\theta\}) - \mathbf T}({\mathbf r_p} + {\mathbf R}_p\{\zeta,\eta,\theta\})]^2$](img63.gif) |
|
|
|
|
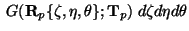 |
|
|
(11) |
Integration is performed over the parts of space where
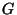 has been chosen to be
nonzero.
We now instantiate
has been chosen to be
nonzero.
We now instantiate
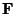 and
and
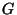 in the local (rotated and
translated) frame of reference. These can be thought of as functions
of
in the local (rotated and
translated) frame of reference. These can be thought of as functions
of
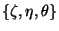 only, since
only, since
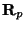 is independent
of the integration variables.
For
is independent
of the integration variables.
For 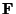 we will use a polynomial function of degree
we will use a polynomial function of degree
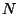 in the
variables
in the
variables 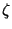 ,
, 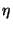 and
and
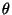 :
:
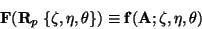 |
(12) |
where
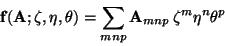 |
(13) |
Figure 5:
Oriented moving least squares (MLS) tensor filter. The smallest ellipsoids represent the interpolated tensor data; the largest ellipsoid represents the domain of the moving filter
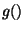 described in Eq.
described in Eq.
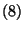 ; the dark ellipsoid represents the computed filtered tensor. The filter travels continuously along the fiber line; grid shows initial sampling of the tensor data.
; the dark ellipsoid represents the computed filtered tensor. The filter travels continuously along the fiber line; grid shows initial sampling of the tensor data.
To instantiate 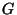 , we also use a function of variables
, we also use a function of variables
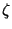 ,
, 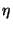 and
and 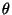 :
:
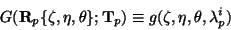 |
(14) |
The function g() is clipped to zero at some low threshold value to
create a finite integration volume and
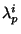 are eigenvalues of the tensor
are eigenvalues of the tensor
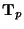 .
Substituting expressions (13) and (14) into the equation (11) we get:
.
Substituting expressions (13) and (14) into the equation (11) we get:
|
![$\displaystyle E = \int_V {[\sum_{mnp} {\mathbf A}_{mnp}
~\zeta^m \eta ^n \theta^p - \mathbf T}({\mathbf r_p} + {\mathbf R}_p\{\zeta,\eta,\theta\})]^2$](img75.gif) |
|
|
|
|
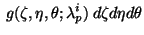 |
|
|
(15) |
The least squares fitting procedure reduces to minimizing functional
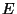 with respect to tensor elements
with respect to tensor elements
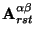 .
To do this we differentiate the expression (11) with
respect to each one of the
.
To do this we differentiate the expression (11) with
respect to each one of the
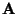 coefficients, equate the result
to zero, and linearly solve to find the unknown
coefficients, equate the result
to zero, and linearly solve to find the unknown
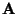 's:
's:
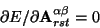 |
(16) |
This gives us the following linear system for the unknown
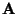 's:
's:
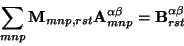 |
(17) |
where
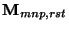 are elements of the matrix;
are elements of the matrix;
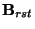 are right hand side values of the equation:
are right hand side values of the equation:
These integrals can be computed numerically or any specific choice of
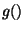 .3
The equation (17) is just a ``regular'' linear system to
find the
.3
The equation (17) is just a ``regular'' linear system to
find the 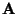 's. Written out component-wise for the
tensors
's. Written out component-wise for the
tensors 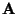 ,
,
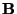 and
and
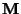 with contracted
indexing it becomes
with contracted
indexing it becomes
This system is also known as a system of ``normal equations'' for the
least squares optimization
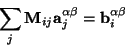 |
(21) |
The optimization procedure allows as to compute the polynomial
coefficients for best approximation of the tensor data within a region
of a chosen point by a chosen degree of polynom. Then the value at the
point 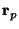 , which is the origin in the
, which is the origin in the
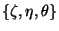 frame of reference, can be easily calculated using (13):
frame of reference, can be easily calculated using (13):
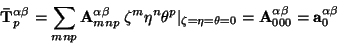 |
(22) |
It is important to notice, that the value of
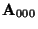 depends on the order of polynomial used for fitting.
We also notice, that using a zero-order polynomial approximation
(i.e.,
depends on the order of polynomial used for fitting.
We also notice, that using a zero-order polynomial approximation
(i.e., 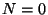 ) is equivalent to finding a weighted average of a tensor
function within the filter volume:
) is equivalent to finding a weighted average of a tensor
function within the filter volume:
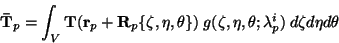 |
(23) |
The major advantage of the higher order approximation is that it better
preserves the absolute magnitude of the feature in the areas which have
maxima or minima, compared to simple averaging, which tends to lower the
height of the maxima and the depth of the minima.
Finally, for the filter function
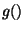 , we have chosen an anisotropic
Gaussian weighting function
, we have chosen an anisotropic
Gaussian weighting function
 with axes aligned along the
eigenvector directions and ellipsoidal semi-axes (the radii)
proportional to the square root of corresponding eigenvalues.
with axes aligned along the
eigenvector directions and ellipsoidal semi-axes (the radii)
proportional to the square root of corresponding eigenvalues.
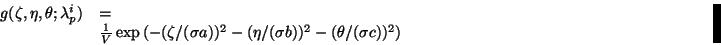 |
(24) |
with
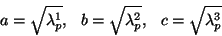 |
(25) |
The variable
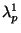 is the largest eigenvalue of the diffusion
tensor
is the largest eigenvalue of the diffusion
tensor 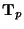 at the location
at the location
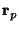 ,
,
 is the second largest, etc. The value
is the second largest, etc. The value
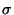 is a parameter that can
enlarge or contract all of the ellipsoid radii. It is important to
notice, that since we are trying to trace fibers, i.e., to extract
structures with a very strong directional information, the filter is
typically much more influenced by the data points ``in front'' and
``behind'' but not on the side. Thus, usually,
is a parameter that can
enlarge or contract all of the ellipsoid radii. It is important to
notice, that since we are trying to trace fibers, i.e., to extract
structures with a very strong directional information, the filter is
typically much more influenced by the data points ``in front'' and
``behind'' but not on the side. Thus, usually,
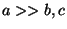 .
Also note that in the equation for the filter function
.
Also note that in the equation for the filter function
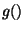 (25), we have a choice of values for the diffusion tensor
(25), we have a choice of values for the diffusion tensor
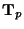 . In our algorithm we use the filtered tensor value
from the previous time step,
. In our algorithm we use the filtered tensor value
from the previous time step,
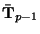 , to determine the
weighting function ellipsoid to use for the current time step.
, to determine the
weighting function ellipsoid to use for the current time step.
Next: Streamline Integration
Up: Method
Previous: Data Interpolation
Leonid Zhukov
2003-01-05
![]() , the tensor function
, the tensor function
![]() is a
linear combination of tensor basis functions we will use to fit the data. The
function
is a
linear combination of tensor basis functions we will use to fit the data. The
function ![]() is the moving and rotating anisotropic filtering window,
centered at the point
is the moving and rotating anisotropic filtering window,
centered at the point
![]() (See Figure 4.)
We felt it was more convenient to perform the computations in the
local frame of reference connected to a particular filtering window,
rather than in world coordinates. It is straightforward to transform
equation (8) to a local frame of reference using a
change of variables involving the following translation and rotation
transformation:
(See Figure 4.)
We felt it was more convenient to perform the computations in the
local frame of reference connected to a particular filtering window,
rather than in world coordinates. It is straightforward to transform
equation (8) to a local frame of reference using a
change of variables involving the following translation and rotation
transformation:
![]() described in Eq.
described in Eq.
![]() ; the dark ellipsoid represents the computed filtered tensor. The filter travels continuously along the fiber line; grid shows initial sampling of the tensor data.
; the dark ellipsoid represents the computed filtered tensor. The filter travels continuously along the fiber line; grid shows initial sampling of the tensor data.![]() , we also use a function of variables
, we also use a function of variables
![]() ,
, ![]() and
and ![]() :
: