Source localization For each electrode potential map  , we can now localize a single dipole using a search method to minimize Eq. (6). We have chosen to use the straight-forward downhill simplex search. Since we know we are only searching for one dipole source which produced each activation map,  , we will only need to optimize six degrees of freedom: the position (x, y, z), orientation  and strength P of a single dipole. The last three variables can be thought of as components  , the dipole strength in the x, y and z direction. Since the potential is a linear function of dipole moment, we can further reduce our search space by using the analytic optimization from [34, 35]. Specifically, for each location to be evaluated for the simplex, we separately compute the solutions due to dipoles oriented in the x, y and z directions, and solve a  system to determine the optimal strength and orientation for that position [37]. The minimization cost function now explicitly depends on only the coordinates of the dipole    To perform non-linear minimization of R(x,y,z), we applied the multi-start downhill simplex method [21, 36], as implemented in [38]. In an N-dimensional space, the simplex is a geometric figure that consists of N+1 fully interconnected vertices. In our case we are searching a three-dimensional coordinate space, so the simplex is just a tetrahedron with four vertices. The downhill simplex method searches for the minimum of the three-dimensional function by taking a series of steps, each time moving a point in the simplex (a dipole) away from where the function is largest (see Fig. 10). The single dipole solution to the source localization problem is unique [39]. This follows from the fundamental physical properties of the model and can be illustrated by considering the cost function Eq. (6) over its entire three-dimensional domain. A computationally efficient method for evaluating the cost function using lead-field theory is discussed in [37]. However, despite the uniqueness of the solution, in the case of linear finite elements the downhill simplex search method may fail to reach the global minimum. This can happen when the nodes of the simplex (and its attempted extensions) are all contained within a single element of the finite element model. In such situations, the simplex must be restarted several times in order to find the true global minimum. After all of the dipoles have been localized, the only step which remains is to determine their absolute strengths. This can be accomplished by solving a small,  , linear minimization problem, where m is the number of dipoles. For this study, we recovered three dipoles, so we solved a  system, where the right hand side is formed by the inner products of optimized single dipole solutions and EEG recordings  .     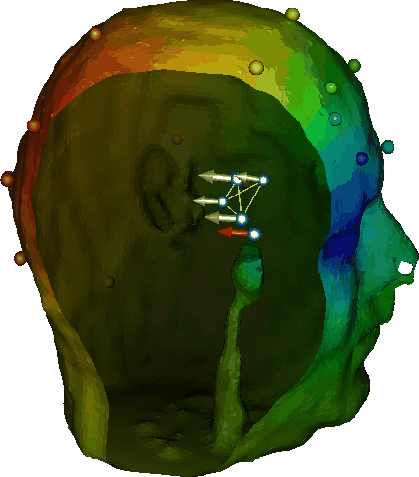Figure 10: Visualization of the downhill simplex algorithm converging to a dipole source. The simplex is indicated by the gray vectors joined by yellow lines. The true source is indicated in red. The surface potential map on the scalp is due to the forward solution of one of the simplex vertices, whereas the potentials at the electrodes (shown as small spheres) are the ``measured'' EEG values (potentials due to the true source).          Fri Oct 8 13:55:47 MDT 1999

 
Revised: March , 2005