Next: Forward Problem Up: Independent Component Analysis For Previous: Independent Component Analysis For
Introduction
Electroencephalography (EEG) is a technique for the non-invasive characterization of brain function. Scalp electric potential distributions are a direct consequence of internal electric currents associated with neurons firing and can be measured at discrete recording sites on the scalp surface over a period of time.Most measured, non-background brain activity is generated within the
cerebral cortex, the outer surface (1.5-4.5 mm thick) of the brain comprised
of approximately ten billion neurons. The active regions within the cortex
are generally fairly well localized, or focal. Their activity is
the result of synchronous synaptic stimulation of a very large number ![]() of neurons. Cortical neurons align themselves in columns oriented orthogonally
to the cortical surface [1]. When a
large group of such neurons all depolarize or hyperpolarize in concert,
the result is a dipolar current source oriented orthogonal to the cortical
surface. It is the propagation of this current that we measure using EEG.
of neurons. Cortical neurons align themselves in columns oriented orthogonally
to the cortical surface [1]. When a
large group of such neurons all depolarize or hyperpolarize in concert,
the result is a dipolar current source oriented orthogonal to the cortical
surface. It is the propagation of this current that we measure using EEG.
Estimation of the location and distribution of current sources within
the brain based on potential recordings from the scalp (source localization)
is one of the fundamental problems in electroencephalography. It requires
the solution of an inverse problem, i.e., given a subset of electrostatic
potentials measured on the surface of the scalp, and the geometry and conductivity
properties within the head, calculate the current sources and potential
fields within the cerebrum. This problem is challenging because solutions
do not depend continuously on the data and because it lacks a unique solution.![]() The lack of continuity implies that small errors in the measurement of
the voltages on the scalp can yield unbounded errors in the recovered solution.
The non-uniqueness is a consequence of the linear superposition of the
electric field: different internal source configurations can produce identical
external electromagnetic fields, especially when only measured at a finite
number of electrode positions [1, 3,
4].
The lack of continuity implies that small errors in the measurement of
the voltages on the scalp can yield unbounded errors in the recovered solution.
The non-uniqueness is a consequence of the linear superposition of the
electric field: different internal source configurations can produce identical
external electromagnetic fields, especially when only measured at a finite
number of electrode positions [1, 3,
4].
However, if accurate solutions to such problems could be obtained, neurologists would gain non-invasive access to patient-specific cortical activity. Access to such data would ultimately increase the number of patients who could be effectively treated for pathological cortical conditions such as epilepsy [5, 6].
There exist several different approaches to solving the source localization problem. Initially, many of these were implemented on spherical models of the head [7, 8]. Those methods that proved promising were then extended to work on realistic geometry [9]. One of the most general methods for inverse source localization involves starting from some initial distributed estimate of the source and then recursively enhancing the strength of some of the solution elements, while decreasing the strength of the rest of the solution elements until they become zero. In the end, only a small number of elements will remain nonzero, yielding a localized solution. This method is implemented, for example, in the FOCUSS algorithm [10]. Another example of an iterative re-weighting technique is the LORETA algorithm [11].
A second source localization approach incorporates a priori assumptions about sources and their locations in the model. Electric current dipoles are usually used as sources, provided that the regions of activations are relatively focused [3]. Although a single dipole is the most widely used model, it has been demonstrated that a multiple dipole model is required to account for a complex field distribution on the surface of the head [12]. If the distance between the dipoles is large or the dipoles have entirely different temporal behavior, the field patterns may exhibit only minor overlap and they can be fit individually using the single-dipole model. However, more often than not, examination of spatial surface topographies can be misleading, as the time series of multiple dipoles overlap and potentials cancel each other out [4, 13]. In such cases, one must employ a third approach: a spatio-temporal model.
The main assumption of this model is that there are several dipolar sources that maintain their position and orientation, and vary just their strength (amplitude) as a function of time. Now, rather than fit dipoles to measurements from one instant in time, dipoles are fit by minimizing the least-square error residual over the entire evoked potential epoch [14].
A more advanced version of this spatio-temporal approach is developed in the multiple signal classification algorithm, MUSIC [15], and in its extension, RAP-MUSIC [16]. A signal subspace is first estimated from the data and the algorithm then scans a single dipole model through the three-dimensional head volume and computes projections onto this subspace. To locate the source, the user must search the head volume for local peaks in the projection metric. The RAP-MUSIC extension of this algorithm automates this search, extracting the location of the sources through a recursive use of subspace projection.
While the above methods represent significant advances in source localization, they fail to address the problem most recently identified by Cuffin in [17]: ``Solutions to multiple dipole ... sources are much less reliable than solutions for single-dipole sources. These solutions can be very sensitive to ... noise. At present, this sensitivity limits the usefulness of these solutions as clinical and research tools.'' In this paper, we introduce a novel approach for spatio-temporal source localization of independent sources. In our method, we first separate the raw EEG data into independent sources. We then perform a separate localization procedure on each independent source. Because we localize sources independently, our method is just as reliable as single dipole source localization methods.
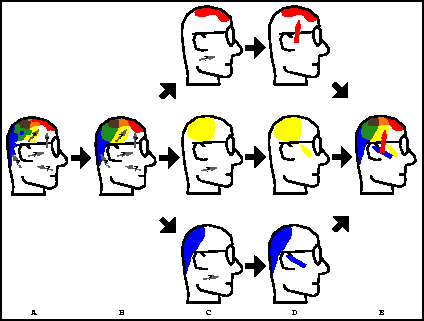
Figure 1: A depiction of the steps of our algorithm. A) Measured
signals are recorded at the scalp surface through EEG electrodes; the underlying
neural sources (which we will model as dipoles) are unknown. B) With PCA
decomposition, truncation, and reconstruction, much of the noise is removed
from the EEG data. C) Using the ICA algorithm, the time signals can be
decomposed into statistically independent activation maps (summing these
activation maps returns the original measured signals). C) For each independent
activation map, the single dipole source that best accounts for the map's
voltages is localized. D) Integrated together, these independent dipole
sources reproduce the signal from B).
The steps of our method are depicted in Fig. 1. We begin by extracting the signal subspace of the EEG data using a Principal Component Analysis (PCA) algorithm. This step removes much of the noise from the data and reduces its dimensionality by truncating lower order terms of the decomposition (i.e., discarding the noise subspace). We then divide the PCA signal subspace into several components, using the recently developed Independent Component Analysis (ICA) [18, 19, 20] signal processing technique. The result of this preprocessing is a set of time-series signals (which sum to the original signal) at each electrode, where each time-series corresponds to an independent source in the model. The number of different maps created by ICA is equal to the number of temporally independent, stationary sources in the problem. To localize each of these independent sources, we solve a separate source localization problem. Specifically, for each independent component, we employ a downhill simplex search method [21] to determine the dipole which best accounts for that particular component's contribution of the signal.
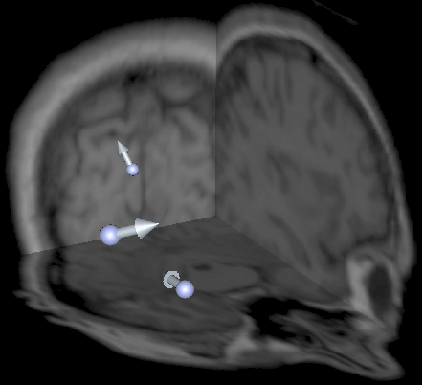
Figure 2: Distribution of dipole sources (arrows) visualized
with orthogonal MRI slices (background).
In our study we use simulated data obtained by placing dipoles in a computational model at positions corresponding to observed epileptic sources in children with Landau-Kleffner syndrome [6]. We chose to simulate three tangential epileptogenic right-hemisphere sources, as shown in Fig. 2: the first in the temporal lobe, the second in the occipital lobe, and the third in the Sylvian fissure. This distributed configuration is typical of multifocal epilepsy, where each source has an independent time course [6]. For each of these sources, we use a time signal from a clinical study to its magnitude over time. That is, we place the three current dipoles inside our finite element model, and for each instant in time, we project the activation signals onto 32 clinically measured scalp electrode positions and add 2% noise to the signals. The electrode positions are shown in Fig. 3. Projecting the sources onto the electrodes requires the solution of a so-called forward problem.
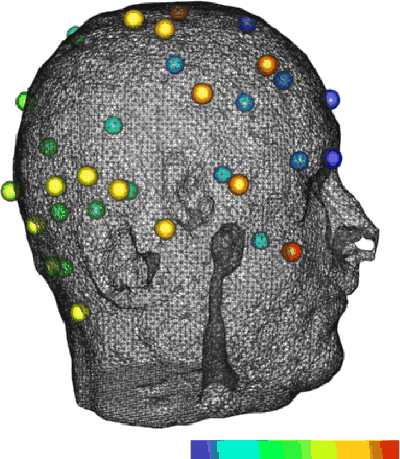
Figure 3: Triangulated scalp surface with 32 electrodes. The
electrodes have been color-mapped to indicate order: they are colored from
blue to red as the channel number increases.
Next: Forward Problem Up: Independent Component Analysis For Previous: Independent Component Analysis For Zhukov Leonid
Fri Oct 8 13:55:47 MDT 1999