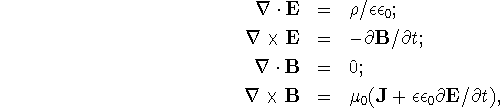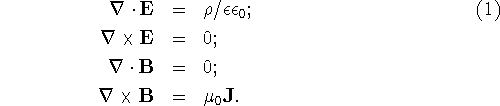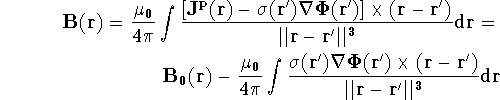Physics of EEG/MEG

We consider a head to be  a volume conductor with a nonuniform anisotropic conductivity tensor , and a magnetic permeability of free space .

In general, electromagnetic field in the media is described by the system of Maxwell equations:

where and are electric and magnetic fields, J is the current density and is the permitivity of the media.

Another important equation is the continuity equation:

where is an electric charge density.

In neuromagnetism, frequencies are usually below 100Hz and electric and magnetic field time derivatives are typically much smaller than ohmic currents, so we can neglect the displacement current and the non-potentiality of the field . Thus, below we will be using a quasi-static approximation of Maxwell's equations:

and

 

(this last equation simply states that the sum of all the currents entering the volume is zero, or Kirkoff's second law).

It is convenient to split the total current into - primary current, or current from the sources, and , secondary or return current. The primary current (sources) creates electric field which causes secondary current . Then

 

 

Substituting this equation into continuity equation (2), we get

 

 

Since , the electric field can be represented as a gradient of some potential

 

Substituting this expression into Eq.(4) we get

 

which is a Poisson's equation for an electric potential.

The second Maxwell's equation, together with the continuity equation

provides boundary conditions on the boundary interface between two media

Since we consider a boundary between a conducting media and an insulator (in the air ), the boundary conditions will read

Assuming no current sources in the surface layer . This gives us the boundary condition for the Poisson equation

 

on the outside surface (scalp).

There is no current outside of the media, but there still exists the tangential electric field which decays with distance. Since the surface shape is non-trivial, the solution of Eq. (6) with boundary conditions Eq. (7) can only be found numerically.

Since the divergence of a magnetic field is always zero (no magnetic monopoles exists), , the magnetic field can be represented as a curl of some vector , where is called a vector potential. Substitution of this expression in the last Maxwell's equation leads to

Using vector calculus we get

Vector potential is defined up to a gauge. Choosing the ``Coulomb gauge'' we set =0 and simplify the last equation to

This is again a Poisson's equation, but now with a different set of boundary conditions. Since magnetic permeability of the media is the same as of the air, there is no boundary conditions exists for the magnetic field. The only physical condition will be that , no magnetic field at infinity. In this case the Poisson's equation can be solved analytically and the solution for the vector potential is well known and given by the following integral:

where integration is over the entire volume space (currents are non-zero only inside the head!). After taking the curl we get the expression for the magnetic field

Substituting current from Eq.(3,5) into the above formula we get

where

Applying differentiation by parts and assuming zero conductivity outside the surface, we can rewrite the above integral as

It is clear from the last expression, that if were constant, then the magnetic field would only be due to the primary source currents. If can be considered piece-wise constant within certain areas, then the above integral will be non-zero only on the boundary between those areas and can easily be reduced to a sum of the surface integrals over those surfaces. In our case, though, is anisotropic and varies continuously in space, so we have to compute the second integral explicitly.

The primary current density can be approximated by a current dipole which is a unidirectional line element of current pumped from a ``sink'' to a ``source''. The convenient mathematical representation for the the current density can be given through the Dirac delta function (point source)

where is a current dipole. It can also be interpreted as - dipole current I times the distance between the ``source'' and the ``sink'. Then the Poisson equation (6) will become

 

Finally, we can summarize the algorithm for the solution of EEG/MEG forward problems:

• EEG forward problem
  • Set up current sources ;
  • Solve with boundary conditions;
  • Find potentials on the scalp.
• MEG forward problem
  • Repeat first two steps from the above;
  • Compute conduction current
  • Compute ;
  • Find components of field at the desired positions.

 

 

 
Revised: March , 2005