Tensor invariants (rotational invariants) are combinations of tensor
elements that do not change after the rotation of the tensor's frame
of reference, and thus do not depend on the orientation of the patient
with respect to the scanner when performing DT imaging.
The well known invariants are the eigenvalues of diffusion tensor
(matrix) ![]() , which are the roots of corresponding characteristic equation
, which are the roots of corresponding characteristic equation
|
|
|
|
|
|
|
|
|
(5) |
|
|
|
|
Any combination of the above invariants is, in turn, an invariant. We
consider the following dimensionless combination:
![]() . In
the eigenvector frame of reference it becomes
. In
the eigenvector frame of reference it becomes
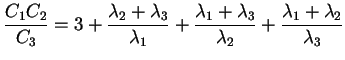 |
(6) |
It is easy to show that for isotropic diffusion, when
![]() , the coefficient
, the coefficient
![]() . In the anisotropic case, this measure is
identical for both linear, directional diffusion
. In the anisotropic case, this measure is
identical for both linear, directional diffusion
![]() and planar diffusion
and planar diffusion
![]() and is equal to
and is equal to
![$\displaystyle C_a^{limit} \approx \frac{1}{3}\left[1 + \frac{\lambda_1}{\lambda_3} + \frac{\lambda_3}{\lambda_1}\right].$](img40.gif) |
(8) |
Thus ![]() is always
is always
![]() and measures
the magnitude of the diffusion anisotropy. We again want to
emphasize, that we use eigenvalue representation here only to analyze
the behavior of the coefficient
and measures
the magnitude of the diffusion anisotropy. We again want to
emphasize, that we use eigenvalue representation here only to analyze
the behavior of the coefficient
![]() , but we use invariants
, but we use invariants
![]() to compute it using Equations (5) and (7).
to compute it using Equations (5) and (7).
Figure 2. Isotropic
![]() (left) and anisotropic
(left) and anisotropic
![]() (right)
tensor invariants for the tensor slice shown in Figure
1.
(right)
tensor invariants for the tensor slice shown in Figure
1.