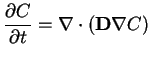 |
(1) |
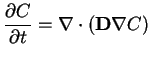 |
(1) |
|
|
(2) |
Tissue segmentation and classification based on DT-MRI offers several advantages over conventional MRI, since diffusion data contains additional physical information about the internal structure of the tissue being scanned. However, segmentation and visualization using diffusion data is not entirely straightforward. First of all, the diffusion matrix itself is not invariant with respect to rotations, and the elements that form the matrix will be different for different orientations of the sample or field gradient and therefore cannot themselves be used for classification purposes. Moreover, 3D visualization and segmentation techniques available today are predominantly designed for scalar and sometimes vector fields. Thus, there are two fundamental problems in tensor imaging: a) finding an invariant representation of a tensor that is independent of a frame of reference and constructing a mapping from the tensor field to a scalar or vector field, and b) visualization and classification of tissue using the derived scalar fields.
The traditional approaches to diffusion tensor imaging involve converting the tensors into an eigenvalue/eigenvector representation, which is rotationally invariant. Every tensor may then be interpreted as an ellipsoid with principal axes oriented along the eigenvectors and radii equal to the corresponding eigenvalues. This ellipsoid describes the probabilistic distribution of a water molecule after a fixed diffusion time.
Using eigenvalues/eigenvectors one can compute different anisotropy
measures [1,3,4,5] that map tensor data onto scalars and
can be used for further visualization and segmentation. Although
eigenvalue/vector computation of the
![]() x
x![]() matrix is not expensive,
it must be repeatedly performed for every voxel in the volume. This
calculation easily becomes a bottleneck for large datasets. For
example, computing eigenvalues and eigenvectors for a
matrix is not expensive,
it must be repeatedly performed for every voxel in the volume. This
calculation easily becomes a bottleneck for large datasets. For
example, computing eigenvalues and eigenvectors for a
![]() volume
requires over 20 CPU-minutes on a powerful workstation. Another
problem associated with eigenvalue computation is stability - a small
amount of noise will not only change the values but also the ordering
of the eigenvalues[7]. Since many anisotropy measures depend on the
ordering of the eigenvalues, the calculated direction of
diffusion and classification of tissue will be significantly altered
by the noise normally found in diffusion tensor datasets. Thus it is
desirable to have an anisotropy measure which is rotationally
invariant, does not require eigenvalue computations and is stable with
respect to noise. The tensor invariants with these
characteristics were first proposed by Ulug and Zijl[8]. In Section
2 of this paper we
formulate a new anisotropy measure for tensor field based on these invariants.
volume
requires over 20 CPU-minutes on a powerful workstation. Another
problem associated with eigenvalue computation is stability - a small
amount of noise will not only change the values but also the ordering
of the eigenvalues[7]. Since many anisotropy measures depend on the
ordering of the eigenvalues, the calculated direction of
diffusion and classification of tissue will be significantly altered
by the noise normally found in diffusion tensor datasets. Thus it is
desirable to have an anisotropy measure which is rotationally
invariant, does not require eigenvalue computations and is stable with
respect to noise. The tensor invariants with these
characteristics were first proposed by Ulug and Zijl[8]. In Section
2 of this paper we
formulate a new anisotropy measure for tensor field based on these invariants.
Visualization and model extraction from the invariant 3D scalar fields is the second issue addressed in this paper. One of the popular approaches to tensor visualization represents a tensor field by drawing ellipsoids associated with the eigenvectors/values[9]. This method was developed for 2D slices and creates visual cluttering when used in 3D. Other standard CFD visualization techniques like tensor-lines do not provide meaningful results for the MRI data due to rapidly changing directions and magnitudes of eigenvector/values and also amount of noise present in the data. Recently Kindlmann[10] developed volume rendering approach to tensor field visualization using eigenvalue-based anisotropy measures to construct transfer function and color maps, that highlight some brain structures and diffusion patterns.
In our work we perform iso-surfacing on the 3D scalar fields derived from our tensor invariants to visualize and segment the data. An advantage of iso-surfacing over other approaches is that it can provide the shape information needed for constructing geometric models, and computing internal volumes and external surface areas of the extracted regions. A detailed discussion of the modeling method is given in Section 3. Section 4 presents the results of tensor invariant calculations and model segmentation technique with examples from a DT-MRI scan of a human head. Section 5 then describes the quantitative analysis of obtained geometric models.
Finally, there has been a number of recent publications[11,12] devoted to brain fiber tracking. This is a different and more complex task than the one addressed in this paper and requires data with a much higher resolution and better signal-to-noise ratio than the data used in our study.
Figure 1. Slice of a tensor volume where every ``element'' of the
image matrix corresponds to one component of the tensor
![]() .
.